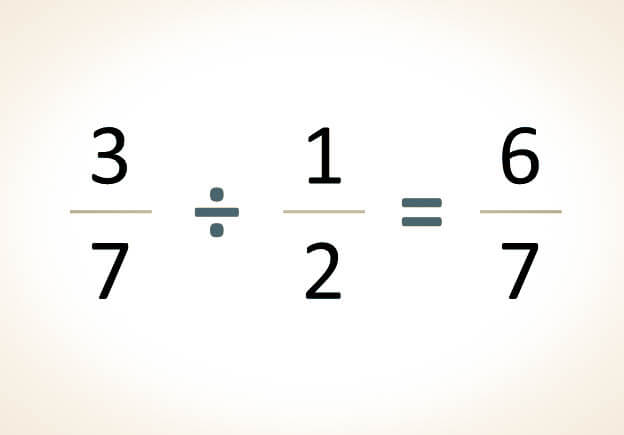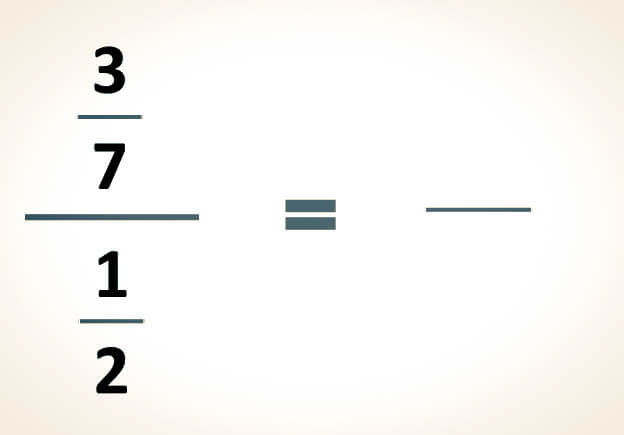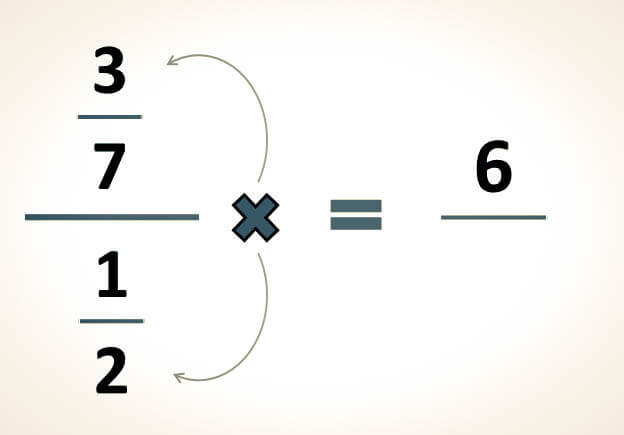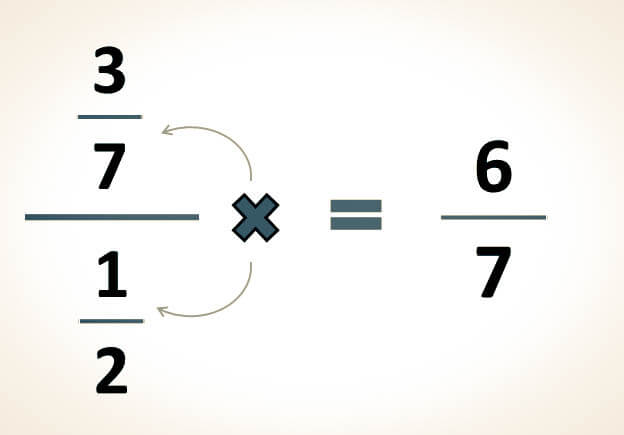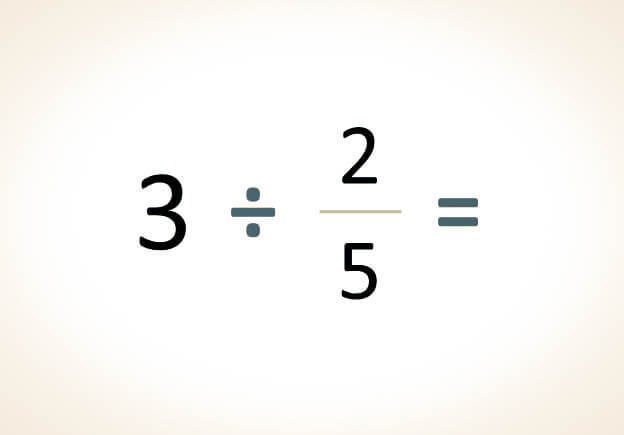División de fracciones

Para realizar una división con fracciones, se procede de manera cruzada multiplicando el numerador por el denominador de la segunda fracción y el primer denominador por el segundo numerador. Luego, se simplifica o reduce el resultado a su forma más simple si es posible.

Este método se aplica indistintamente, ya sea que las divisiones tengan denominadores iguales o diferentes.

Ejemplo

La siguiente división se procederá a resolver mediante el método de productos cruzados.

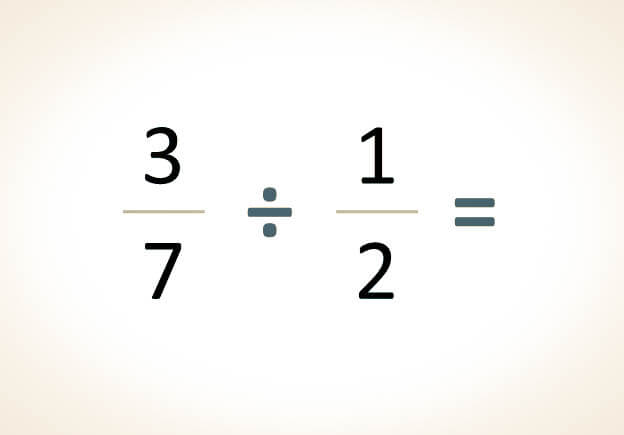
En primer lugar, se realiza la multiplicación del primer numerador por el denominador de la segunda fracción, y se registra el producto como numerador:

    
37


÷

    
12


=

    
3 x 20


=

    
60

En segundo lugar, se realiza la multiplicación del primer denominador por el numerador de la segunda fracción, y se registra el producto como denominador:

    
37


÷

    
12


=

    
3 x 27 x 1


=

    
67

Ya que la fracción obtenida en el paso anterior no se puede simplificar más, se considera como el resultado de la división:

La división de fracciones puede expresarse tanto en formato horizontal como vertical. Cuando se representa en formato vertical, se utiliza la conocida regla del sándwich, que implica multiplicar los extremos entre sí y los medios entre sí para obtener el resultado.

Ejemplo

Para resolver la siguiente división, primero se multiplican los extremos y se registra el producto como numerador. Luego, se multiplican los medios y el resultado se anota como denominador.

Si lo prefiere, puede optar por representar la división vertical de manera horizontal para llevar a cabo su resolución.

    
37


÷

    
12


=

    
3 x 27 x 1


=

    
67

Para realizar la división entre una fracción y un número entero, el proceso implica primero convertir el número entero en una fracción común. Después se procede a resolver la división utilizando el método de productos cruzados o el método del recíproco.

Cabe señalar que la diferencia entre uno y otro método de resolución es que en el primero se realiza la multiplicación en forma cruzada mientras que en el segundo se hace de forma lineal.

Ejemplo

La siguiente división se procederá a resolver mediante el método del recíproco.

Para ello, primero se efectúa la conversión del número entero en una fracción común, para lo cual se coloca el número 3 como numerador y el número 1 como denominador:

Conversión

3

=

    
31

Sustitución

    
31


÷

    
25

Una vez obtenida una división con fracciones, se procede a obtener el recíproco de la segunda fracción. Esto se logra invirtiendo los valores, de modo que el numerador se convierte en denominador y viceversa:

Recíproco

    
25


=

    
52

Sustitución

31
÷
52
=

Finalmente, se lleva a cabo la multiplicación del numerador por numerador y del denominador por denominador para obtener el resultado de la división:

    
31


÷

    
52


=

    
3 x 51 x 2


=

    
152

Para llevar a cabo la división entre una fracción y un número mixto, el proceso implica primero la conversión de la fracción mixta en una fracción impropia.

Una vez realizada la conversión y obtenida una división con fracciones, se puede resolver utilizando cualquiera de los dos métodos anteriormente vistos.

Ejemplo

La siguiente división se procederá a resolver mediante el método de productos cruzados.

Como paso inicial, se procede a la conversión del número mixto en una fracción impropia. Para lograrlo, se multiplica el denominador por el número entero y se le suma el valor del numerador. El resultado se registra en una nueva fracción como numerador, mientras que el denominador se mantiene igual al del número mixto:

Conversión

214
=
2 x 4 + 14
=
94

Sustitución

94
÷
23

Por último se procede a resolver la división multiplicando los valores de ambas fracciones de manera cruzada:

94
÷
23
=
9 x 34 x 2
=
278

Para realizar la división entre una fracción y un número decimal, el proceso implica en primer lugar la conversión del número decimal en una fracción decimal.

Posteriormente se resuelve la división por medio de alguno de los métodos anteriormente vistos.

Ejemplo

La siguiente división se procederá a resolver mediante el método de productos cruzados.

Para comenzar, se procede a convertir el número decimal en su fracción decimal equivalente. Para ello, se escribe como numerador el decimal prescindiendo del punto decimal y como denominador se escribe la unidad seguida de tantos ceros como cifras tenga la parte decimal:

Conversión

4.5
=
4510

Sustitución

4510
÷
54

Después se procede a multiplicar de forma cruzada, escribiendo cada resultado en su lugar correspondiente:

4510
÷
54
=
45 x 410 x 5
=
18050

En este caso, se lleva a cabo la simplificación de la fracción obtenida con el fin de calcular el resultado de la división:

4510
÷
54
=
18050
=
185