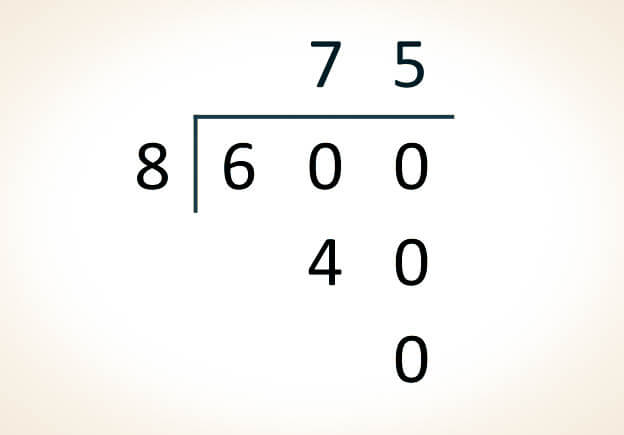
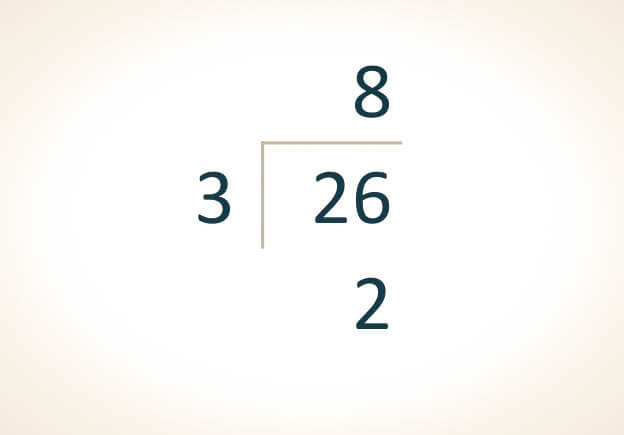Una división se considera exacta si al multiplicar el divisor por el cociente se obtiene el dividendo y, al mismo tiempo, el residuo obtenido es igual a cero.
24 ÷ 3 = 8
Comprobación
3 x 8 = 24
Ejemplo
Si se tienen 24 manzanas y se deben repartir equitativamente entre 3 personas, cada una recibiría 8 manzanas. Es decir, en este caso, es posible dividir el total de manzanas de manera equitativa entre las 3 personas sin que haya sobrantes.
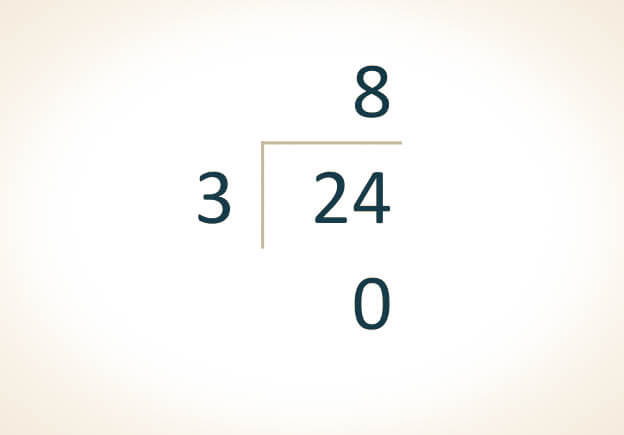
Observaciones
-Una forma clara y sencilla de confirmar si una división es exacta es comprobar si el residuo es igual a cero.