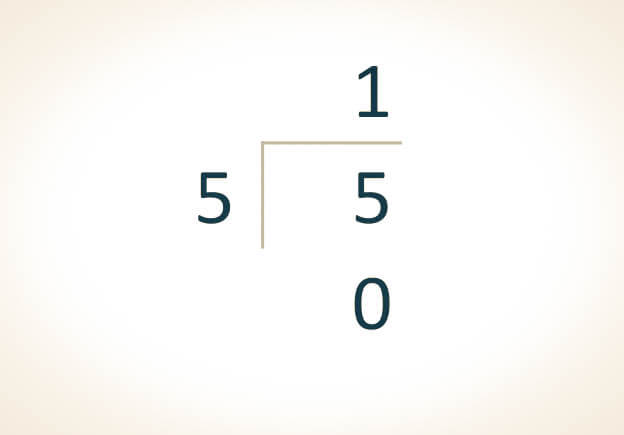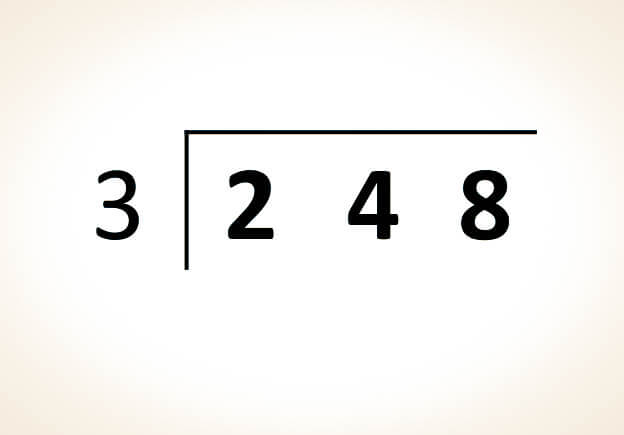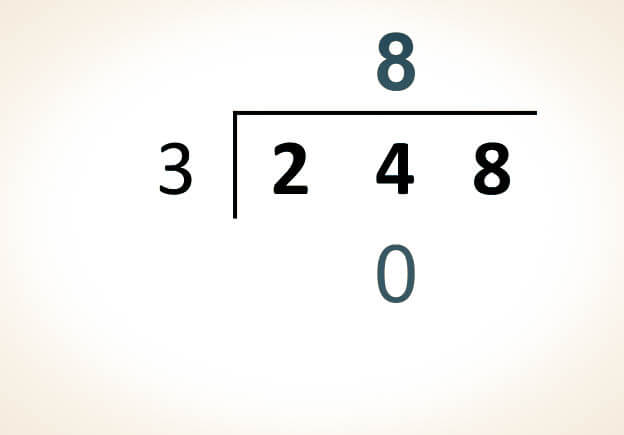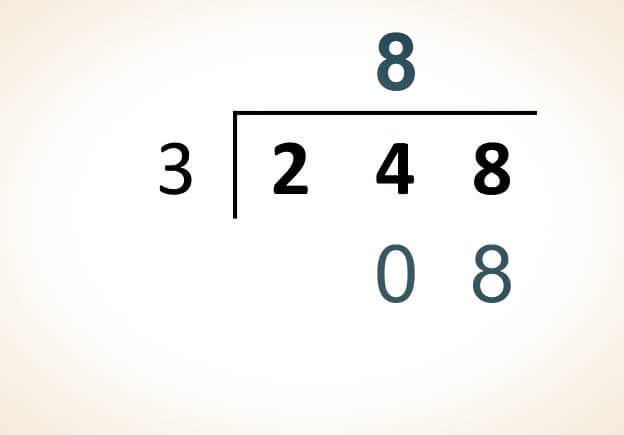PeyemonExisten diversos métodos para resolver la división de números naturales, los cuales varían según el valor del dividendo y divisor.
A continuación, se presentan diferentes tipos de divisiones y se recomienda emplear un método específico de resolución para cada uno de ellos:
Cuando el divisor y el dividendo son iguales, el cociente resultante es uno y el residuo es cero.
Ejemplo
5 ÷ 5 = 1
Cuando el divisor es igual a uno, el cociente es igual al valor del dividendo y el residuo es cero.
Ejemplo
5 ÷ 1 = 5
Cuando el divisor es una potencia de 10 (por ejemplo, 10, 100, 1000, etc.), para obtener el resultado de la división, se procede escribiendo el dividendo y desplazando el punto decimal hacia la izquierda la misma cantidad de lugares que tenga el divisor en ceros.
Si es necesario, se pueden agregar ceros al resultado para completar el número de lugares requeridos.
Ejemplos
Caso 1. Al tener el divisor un solo cero, se debe desplazar el punto decimal del resultado un lugar hacia la izquierda.
586 ÷ 10 = 58.6
Caso 2. Al tener el divisor dos ceros, se debe desplazar el punto decimal del resultado dos lugares hacia la izquierda.
586 ÷ 100 = 5.86
Caso 3. En esta división, al tener el divisor cuatro ceros, se debe desplazar el punto decimal del resultado cuatro lugares hacia la izquierda.
586 ÷ 10000 = 586
Para completar el recorrido, se agrega un cero a la izquierda del resultado, se coloca el punto decimal y se agrega otro cero.
586 ÷ 10000 = 0.0586
Cuando el divisor es un número de un solo dígito, se busca un número que al multiplicarse por el divisor dé como resultado el dividendo de forma exacta o sin excederlo.
Ejemplo
Para realizar la siguiente división:
Se debe comparar el primer dígito del dividendo con el del divisor. Si el dígito del dividendo es mayor o igual al del divisor, se comienza la división utilizando ese dígito. De lo contrario, se debe tomar el siguiente dígito del dividendo hasta que se forme una cantidad mayor o igual al divisor:
| 3 | (2)48 |
En este caso, dado que el divisor (3) es mayor que la primera cifra del dividendo (2), se toma la siguiente cifra del dividendo (4) para formar un número mayor que el divisor.
| 3 | (24)8 |
Dado que el dividendo (24) es mayor que el divisor (3), se procede a buscar un número que, al multiplicarlo por el divisor, nos dé como resultado el número 24 sin excederlo:
3 x 8 = 24
Así, se coloca 8 como cociente y se realiza la resta correspondiente:
24 - 24 = 0
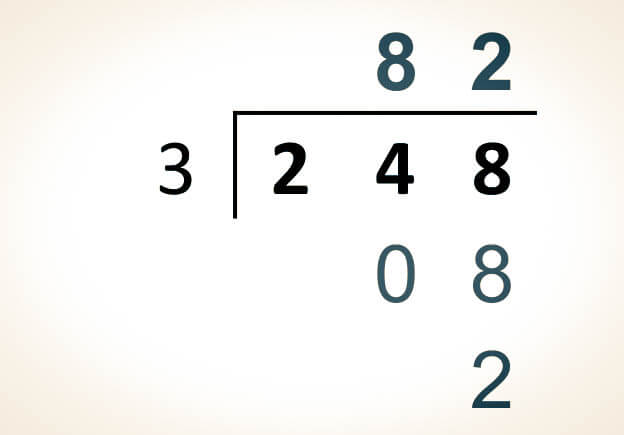
Luego, se baja la siguiente cifra del dividendo (8) para continuar la operación. Es importante tener en cuenta que, si al bajar la cifra, el número formado es menor que el divisor, se escribe cero en el cociente y se procede a bajar la siguiente cifra hasta formar un número mayor que el divisor:
En este caso, se baja el número 8.
El número formado con la cantidad previa del dividendo (08) es mayor que el divisor (3), por lo que se procede a buscar un número que, al ser multiplicado por el divisor, dé como resultado un número igual o menor que 8:
3 x 2 = 6
Se coloca 2 como cociente y se realiza la resta correspondiente:
8 - 6 = 2
Al no haber más cifras en el dividendo, se finaliza la división hasta la parte entera.
A todo este procedimiento de resolución se le conoce como divisiones largas sin resta, ya que no es necesario escribir cada sustracción sino solamente su resultado. Este método es recomendable para simplificar las operaciones realizadas en las divisiones, además de ser ampliamente utilizado.
Cuando el divisor consta de dos o más cifras, el procedimiento de resolución es similar al de la división con un solo dígito. Es decir, se busca un número que, al ser multiplicado por el divisor, dé como resultado una cantidad igual o aproximada a la contenida en el dividendo.
Para llevar a cabo esta operación, se utilizan las tablas de multiplicar del 0 al 9 correspondientes al número que conforma el divisor.
Ejemplo
En este caso, se deben emplear las tablas de multiplicar del número 12 para resolver las operaciones correspondientes a la división previa.
Si el dividendo y el divisor tienen ceros en su parte final, es posible eliminar la misma cantidad de ceros en ambos números sin alterar el resultado de la división.
Ejemplo
| 2400 | 302000 |
En esta división, se pueden suprimir un máximo de dos ceros en ambos números (dividendo y divisor) de forma equitativa. Después de eliminar los ceros, se procede a realizar la división con los números que resultan de la supresión:
Para obtener el residuo final, se le añade la misma cantidad de ceros que se suprimieron previamente, lo que resulta en un residuo de 2000.
